Cauchyho rovnica dynamickej rovnováhy je parciálna diferenciálna rovnica ktorá vychádza zo zachovania hybnosti v kontinuu. Platí pre transport hybnosti v ľubovoľnom kontinuu, kde sa neuplatňujú relativistické javy.
kde ρ je hustota kontinua, 
je tenzor napätia, a 
je vektor objemových síl, obvykle predstavovaných gravitáciou. 
je vektorové pole rýchlostí kontinua a má za premenné čas a súradnice systému.
Po rozložení tenzora napätia na izotropnú a neizotropnú časť, dostaneme:
kde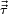 
je tenzor viskózneho (tangenciálneho) napätia a 
je tlak (normálové napätie).
Všetky rovnice popisujúce nerelativistické kontinuum vychádzajú z Cauchyho rovnice dynamickej rovnováhy. Cauchyho rovnica dynamickej rovnováhy je jednou zo základných rovníc popisujúcich transportné fenomény. Pri praktickom použití narážame na prekážky - analytické vyjadrenie tenzora napätia je zolžité, alebo neznáme, preto sa rovnica priamo nepoužíva. Po dosadení patričného vzťahu pre viskozitu dostaneme Navier-Stokesovu rovnicu.
Pokiaľ je kontinuum ideálne (napätie je predstavované len tlakom),
v stacionárnom stave 
a mimo gravitačného pôsobenia (
) dostaneme rovnicu:
Táto rovnica je Bernoulliho rovnica v diferenciálnom tvare a po integrácii dostaneme konvenčný tvar:
Vidíme tak, že Bernoulliho rovnica je dôsledkom zachovávania hybnosti v sústave, ak vyhovuje niektorým zjednodušeniam.
[upraviť] Odvodenie Cauchyho rovnice
Napíšeme si Zákon sily pre element objemu V, ak Σ je plocha, ktorá ho obopína:
Po aplikácii Gaussovej-Ostrogradského vety a sčítaní všetkých zložiek dostaneme
Keďže vektorové pole rýchlosti 
je závislé od polohy aj od času, derivuje sa zložená funkcia:
Po dosadení do odvodenej rovnice zachovania:
[upraviť] Literatúra
- Šesták, J., Rieger, F.: Přenos hybnosti, tepla a hmoty, ČVUT Praha 1998
čítajte viac o Cauchyho rovnica dynamickej rovnováhy